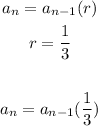Question

27,9,3,1,1/3,1/9....Find the explicit formula for the nth termFind the recursive formula for the nth term

Answer 1

we have the sequence

27,9,3,1,1/3,1/9....

where

a1=27 first term

a2=9

a3=3

a4=1

a5=1/3

a6=1/9

Find out the ratio between consecutive terms

a2/a1=9/27=1/3

a3/a2=3/9=1/3

a4/a3=1/3

a5/a4=1/3/1=1/3

a6/a5=(1/9)/(1/3)=1/3

This is a geometric sequence

The common ratio is r=1/3

Find out the explicit formula for the nth term

The explicit formula is given by the expression

`a_n=a_1(r)^(n-1)`

we have

r=1/3

a_1=27

substitute

`a_n=27((1)/(3))^(n-1)`

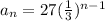
Find out the recursive formula for the nth term

The recursive formula is given by the expression

`\begin{gathered} a_n=a_(n-1)(r) \\ r=(1)/(3) \\ \\ a_n=a_(n-1)((1)/(3)) \end{gathered}`