Question

This is actually a 5 part question, here's the first part.

Answer 1

Since the time of the half-life is 3 hours, then we have to divide the number of hours given by 3

The form of the exponential function is

`D(t)=a(b)^{(t)/(n)}`

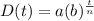
a is the initial amount

b is the factor of increasing or decreasing

In our situation:

Half-life means b = 1/2

Since the initial amount given is 20 mg, then

a = 20

Since the time of half-life is 3 hours, then

t must be the time divided by 3

The function which represents the situation is

`D(t)=20((1)/(2))^{(t)/(3)}`

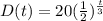
Since t = 3, then

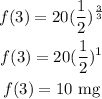
`\begin{gathered} f(3)=20((1)/(2))^{(3)/(3)} \\ f(3)=20((1)/(2))^1 \\ f(3)=10\text{ mg} \end{gathered}`

a.

At t = 6

`\begin{gathered} f((6)/(3))=20((1)/(2))^{(6)/(3)} \\ f(2)=20((1)/(2))^2 \\ f(2)=20((1)/(4)) \\ f(2)=5\text{ mg} \end{gathered}`

At t = 9

`\begin{gathered} f(9)=20((1)/(2))^{(9)/(3)} \\ f(9)=20((1)/(2))^3 \\ f(9)=20((1)/(8)) \\ f(9)=2.5\text{ mg} \end{gathered}`

b.

To find the amount at t = 10 hours, substitute t by 10

`\begin{gathered} f(10)=20((1)/(2))^{(10)/(3)} \\ f(10)=1.98425\text{ mg} \end{gathered}`

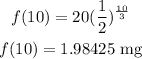
We know that by using the exponential function above

2.

The function form is

`D(t)=A((1)/(2))^{(t)/(n)}`

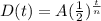
Where A = 20 -------- initial amount

n = 3 ------- the period of half-life

The formula is

`D(t)=20((1)/(2))^{(t)/(3)}`

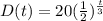
3.

The drug remains after 1 hour means substitute t by 1 first, then divide the answer by the initial amount, and change it to percent

`\begin{gathered} D(1)=20((1)/(2))^{(1)/(3)} \\ D(1)=15.87401052 \end{gathered}`

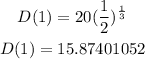
We will find the percent

`\begin{gathered} \text{ \%D=}(15.87401052)/(20)*100\text{ \%} \\ \text{ \%D=79.37\%} \end{gathered}`

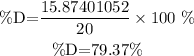
To find the percent of the amount eliminated subtract 79.37% from 100%

`\text{ \%E=100\%-79.37=20.63\%}`

4.

The direction for adults is

Do not exceed 4 doses per 24 hours

5.

Since the table has a period of 2 hours, then we will use t = 2, 4, 6, 8, 10, 12 in the formula above to find the amount of Dex.

`\begin{gathered} D(2)=20((1)/(2))^{(2)/(3)}=12.599\text{ mg} \\ D(4)=20((1)/(2))^{(4)/(3)}=7.937\text{ mg} \end{gathered}`
`\begin{gathered} D(6)=20((1)/(2))^{(6)/(3)}=5\text{ mg} \\ D(8)=20((1)/(2))^{(8)/(3)}=3.150\text{ mg} \end{gathered}`
`\begin{gathered} D(10)=20((1)/(2))^{(10)/(3)}=1.984\text{ mg} \\ D(12)=20((1)/(2))^{(12)/(3)}=1.25\text{ mg} \end{gathered}`