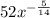Answer
The answer is
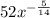
SOLUTION
Problem Statement
We are given the following expression to evaluate:
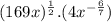
Method
- To solve this question, we need to know some laws of indices. These laws are given below:
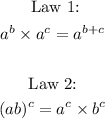
Implementation
Let us apply the law above to solve the question as follows:
![\begin{gathered} (169x)^{(1)/(2)}\text{.}4x^{-(6)/(7)}) \\ By\text{ Law 2, we have:} \\ =169^{(1)/(2)}* x^{(1)/(2)}*4* x^{-(6)/(7)} \\ \\ But\text{ }169^{(1)/(2)}=\sqrt[]{169}=13 \\ 169^{(1)/(2)}* x^{(1)/(2)}*4* x^{-(6)/(7)}=13* x^{(1)/(2)}*4* x^{-(6)/(7)} \\ \\ Collect\text{ like terms} \\ 13*4* x^{(1)/(2)}* x^{-(6)/(7)}=52* x^{(1)/(2)}* x^{-(6)/(7)} \\ \\ By\text{ Law 1, we have:} \\ x^{(1)/(2)}* x^{-(6)/(7)}=x^{(1)/(2)-(6)/(7)}=x^{-(5)/(14)} \\ \\ \therefore52* x^{(1)/(2)}* x^{-(6)/(7)}=52* x^{-(5)/(14)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qsb9gfbjb1pwmxhwr3hm3f1p5insck56qy.png)
Final Answer
The answer is