Solution:
The quadaratic equation is given below as
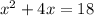
Step 1:
Take half of the x term and square it
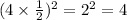
Then add the result to both sides
Hence, We will have
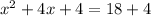
Step 2:
Rewrite the perfect square on the left
Hence,
We will have
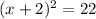
Step 3:
Take the square root of both sides, we will have
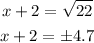
Step 4:
Isolate the x on the left side and
solve for x (1)
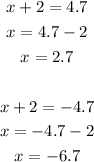
Hence,
The final answers will be shown in the image below