Question

трана s 11 27-1.5 - 10 720 1 0 - Ayo ys agoga vo Anto 36-18-22 А) tarao utas se terre doүчно y-studio Critical thinking questions ту 25) Write a system of equations with the solution (4, -3).

Answer 1

We have to solve the system:

`\begin{gathered} -(5)/(7)-(11)/(7)x=-y \\ 2y=7+5x \end{gathered}`

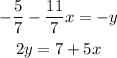
To solve this system by elimination we have to add or substract a linear combination of the second equation from the first equation in order to eliminate one of the variables.

In this case we can multiply the first equation by 2 and add it to the second equation:

`\begin{gathered} -y\cdot2=(-(5)/(7)-(11)/(7)x)\cdot2 \\ -2y=-(10)/(7)-(22)/(7)x \end{gathered}`
`\begin{gathered} -2y+2y=(-(10)/(7)-(22)/(7)x)+(7+5x) \\ 0=-(10)/(7)-(22)/(7)x+7+5x \\ (22)/(7)x-5x=7-(10)/(7) \\ (22x-5\cdot7x)/(7)=(7\cdot7-10)/(7) \\ 22x-35x=49-10 \\ -13x=39 \\ x=(39)/(-13) \\ x=-3 \end{gathered}`

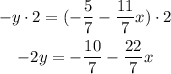
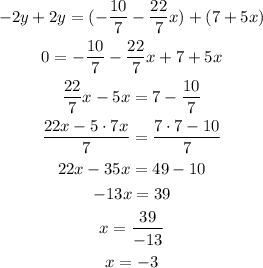
Now we can use any of the two equations to find y:

`\begin{gathered} -y=-(5)/(7)-(11)/(7)x \\ y=(5)/(7)+(11)/(7)(-3) \\ y=(5)/(7)-(33)/(7) \\ y=-(28)/(7) \\ y=-4 \end{gathered}`

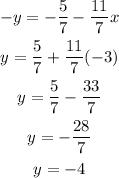
Answer: x=-3 and y=-4