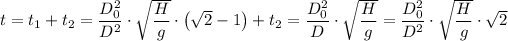Question

The diameter of a cylindrical water tank is Do and its height is H. The tank is filled with water, which is open to the atmosphere. An orifice of diameter D with a smooth entrance (i.e., negligible losses) is open at the bottom. Develop a relation for the time required for the tank (a) to empty halfway (5-point) and (b) to empty completely (5-point).

Answer 1

a. The time required for the tank to empty halfway is presented as follows;

`t_1 = (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) } \cdot \left (√(2) -1 \right)`

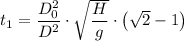
b. The time it takes for the tank to empty the remaining half is presented as follows;

`t_2 = { ( D_0^2 )/(D) \cdot\sqrt{(H)/(g) }`

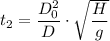
The total time 't', is presented as follows;

`t = √(2) \cdot (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) }`

Step-by-step explanation:

a. The diameter of the tank = D₀

The height of the tank = H

The diameter of the orifice at the bottom = D

The equation for the flow through an orifice is given as follows;

v = √(2·g·h)

Therefore, we have;

`(P_1)/(\gamma) + z_1 + (v_1)/(2 \cdot g) = (P_2)/(\gamma) + z_2 + (v_2)/(2 \cdot g)`

`\left( (P_1)/(\gamma) -(P_2)/(\gamma) \right) + (z_1 - z_2) + (v_1)/(2 \cdot g) = (v_2)/(2 \cdot g)`

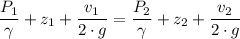
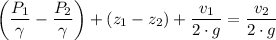
Where;

P₁ = P₂ = The atmospheric pressure

z₁ - z₂ = dh (The height of eater in the tank)

A₁·v₁ = A₂·v₂

v₂ = (A₁/A₂)·v₁

A₁ = π·D₀²/4

A₂ = π·D²/4

A₁/A₂ = D₀²/(D²) = v₂/v₁

v₂ = (D₀²/(D²))·v₁ = √(2·g·h)

The time, 'dt', it takes for the water to drop by a level, dh, is given as follows;

dt = dh/v₁ = (v₂/v₁)/v₂·dh = (D₀²/(D²))/v₂·dh = (D₀²/(D²))/√(2·g·h)·dh

We have;

`dt = (D_0^2)/(D) \cdot(1)/(√(2\cdot g \cdot h) ) dh`

The time for the tank to drop halfway is given as follows;

`\int\limits^(t_1)_0 {} \, dt = \int\limits^h_{(h)/(2) } { (D_0^2)/(D) \cdot(1)/(√(2\cdot g \cdot h) ) } \, dh`

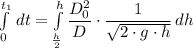
`t_1 =\left[{ (D_0^2)/(D\cdot √(2\cdot g) ) \cdot\frac{h^{-(1)/(2) +1}}{-(1)/(2) +1 } \right]_{(H)/(2) }^(H) =\left[ { (D_0^2 \cdot 2\cdot √(h) )/(D\cdot √(2\cdot g) ) \right]_{(H)/(2) }^(H) = { (2 \cdot D_0^2 )/(D\cdot √(2\cdot g) ) \cdot \left(√(H) - \sqrt{(H)/(2) } \right)`

`t_1 = { (2 \cdot D_0^2 )/(D^2\cdot √(2\cdot g) ) \cdot \left(√(H) - \sqrt{(H)/(2) } \right) = { (√(2) \cdot D_0^2 )/(D^2\cdot √( g) ) \cdot \left(√(H) - \sqrt{(H)/(2) } \right)`

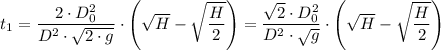
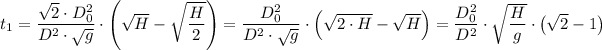`t_1 = { (√(2) \cdot D_0^2 )/(D^2\cdot √( g) ) \cdot \left(√(H) - \sqrt{(H)/(2) } \right) = { (D_0^2 )/(D^2\cdot √( g) ) \cdot \left(√(2 \cdot H) - \sqrt{{H} } \right) =(D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) } \cdot \left (√(2) -1 \right)`The time required for the tank to empty halfway, t₁, is given as follows;

`t_1 = (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) } \cdot \left (√(2) -1 \right)`

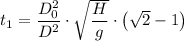
(b) The time it takes for the tank to empty completely, t₂, is given as follows;

`\int\limits^(t_2)_0 {} \, dt = \int\limits^{(h)/(2) }_(0 ) { (D_0^2)/(D) \cdot(1)/(√(2\cdot g \cdot h) ) } \, dh`

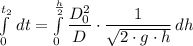
`t_2 =\left[{ (D_0^2)/(D\cdot √(2\cdot g) ) \cdot\frac{h^{-(1)/(2) +1}}{-(1)/(2) +1 } \right]_(0)^{(H)/(2) } =\left[ { (D_0^2 \cdot 2\cdot √(h) )/(D\cdot √(2\cdot g) ) \right]_(0 )^{(H)/(2) } = { (2 \cdot D_0^2 )/(D\cdot √(2\cdot g) ) \cdot \left( \sqrt{(H)/(2) } -0\right)`

`t_2 = { ( D_0^2 )/(D) \cdot\sqrt{(H)/(g) }`

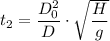
The time it takes for the tank to empty the remaining half, t₂, is presented as follows;

`t_2 = { ( D_0^2 )/(D) \cdot\sqrt{(H)/(g) }`

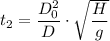
The total time, t, to empty the tank is given as follows;

`t = t_1 + t_2 = (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) } \cdot \left (√(2) -1 \right) + t_2 = { ( D_0^2 )/(D) \cdot\sqrt{(H)/(g) } = (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) } \cdot √(2)`

`t = √(2) \cdot (D_0^2 )/(D^2 ) \cdot \sqrt{ (H)/(g) }`