Question

For each system to the best description of a solution if applicable give the solution

Answer 1

System A

`\begin{gathered} x-4y=4 \\ -x+4y+4=0 \end{gathered}`

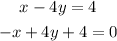
solve the first equation for x

`x=4+4y`

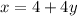
replace in the second equation

`\begin{gathered} -(4+4y)+4y+4=0 \\ -4-4y+4y+4=0 \\ 0=0 \end{gathered}`

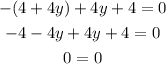
The system has infinitely many solutions, They must satisfy the following equation

`\begin{gathered} x-4y=4 \\ -4y=4-x \\ y=(4)/(-4)-(x)/(-4) \\ y=(x)/(4)-1 \end{gathered}`

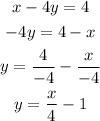
System B

`\begin{gathered} x-2y=6 \\ -x+2y=6 \end{gathered}`

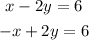
solve for x for the first equation

`x=6+2y`

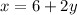
replace in the second equation

`\begin{gathered} -(6+2y)+2y=6 \\ -6-2y+2y=6 \\ -6=6 \end{gathered}`

The system has no solution.