Question

`y \leqslant 4x + 1`graph the inequality

Answer 1

To graph a linear equality in two variables (x and y), we must first proceed as though we are graphing a straight line equation.

Thus, to graph the linear inequality given as:

`y\ge\text{ }(-2)/(3)x\text{ - 1}`

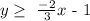
We must first attempt to graph the straight-line equivalent of the inequality given as:

`y=(-2)/(3)x\text{ - 1}`

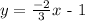
Now to do this, we simply need to find two points that lie on the straight line (since two points are enough to define any straight line),

These points will be the x- and y-intercepts (for the simplicity of this solution)

Now to get the x-intercept, we simply set y to zero and find the corresponding value of x. This is done as follows:

`\begin{gathered} y=(-2)/(3)x\text{ - 1} \\ \text{when y=0} \\ 0=(-2)/(3)x\text{ - 1} \\ \text{multiply through by 3, this gives} \\ 0=-2x\text{ - }3 \\ \text{add 3 to both sides of the equation,} \\ 3+0=-2x-3+3 \\ 3=-2x+0 \\ 3=-2x \\ \text{divide both sides by -2:} \\ (3)/(-2)=(-2x)/(-2) \\ (3)/(-2)=x \\ x\text{ =}(-3)/(2) \end{gathered}`

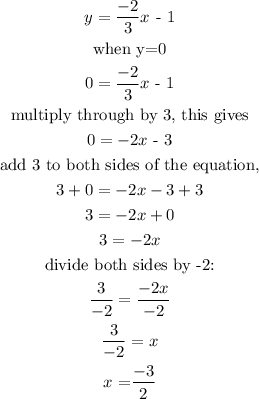
Therefore, the x-intercept is x = -3/2 when y= 0. This is best written in coordinate form as (-3/2, 0)

Now to get the y-intercept, we simply set x to zero and find the corresponding value of y. This is done as follows:

`\begin{gathered} y=(-2)/(3)x\text{ - 1} \\ \text{when x =0} \\ y=(-2)/(3)(0)\text{ - 1} \\ y=\text{ 0 - 1} \\ y=\text{ -1} \end{gathered}`

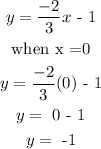
Therefore, the y-intercept is y = -1 when x= 0. This is best written in coordinate form as (0, -1)

Now we will make use of these two coordinates (the x- and y-intercepts) as we plot the graph for the straight line.

This is done in the plot below:

Now, we can now plot the graph of the inequality: