In the given right triangle,
BC=5
AC=12.
Hypotenuse of the triangle, AB=13.
Now, the ratio of sin A can be expressed as,
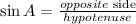
The opposite side to angle A is BC.
Hence,
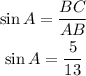
The ratio of cos A can be expresssed as,
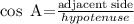
The side adjacent to angle A is AC.
Hence,
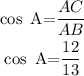
The ratio tan A can be expressed as,
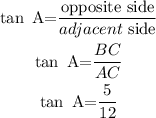
Therefore, sin A=5/13, cos A=12/13 and tan A=5/12.