Question

I have trouble with system of equations. I always get one right and one wrong

Answer 1

`\begin{gathered} x-2y=-2 \\ -x+2y-2=0 \end{gathered}`

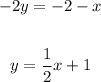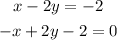
To solve the system of equations above:

1. Rewrite the second equation to be similar to the frist equation:

`\begin{gathered} \text{Add 2 in both sides of the equation:} \\ -x+2y-2+2=0+2 \\ -x+2y=2 \end{gathered}`

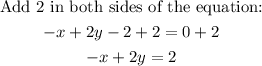
2. Multiply the equation you get in step 1 by -1:

`\begin{gathered} -1(-x+2y=2) \\ x-2y=-2 \end{gathered}`

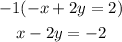
As you get that both equations in the system are the same (x-2y= -2) (the lines are the same) the system has infinitely many solutions (all the values of x and y are solutions for the system)

`\begin{gathered} -2y=-2-x \\ \\ y=(1)/(2)x+1 \end{gathered}`