The standard deviation here uses the sample standard deviation formula:
![s=\sqrt[]{\frac{\sum^{}_i(x_i-\bar{x})^2}{n-1}}](https://img.qammunity.org/2023/formulas/chemistry/college/b59i6gkd5z1od7aeusqlx1bzynaswp7wxl.png)
So, first we make the difference between the values and the mean:
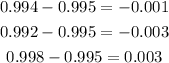
Now, we square them:
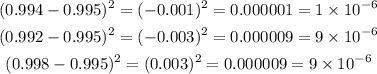
And their sum goes into the equation:
![\begin{gathered} \sum ^{}_i(x_i-\bar{x})^2=1*10^(-6)+9*10^(-6)+9*10^(-6)=1.9*10^(-5) \\ s=\sqrt[]{\frac{\sum^{}_i(x_i-\bar{x})^2}{n-1}}=\sqrt[]{(1.9*10^(-5))/(3-1)}=\sqrt[]{(1.9*10^(-5))/(2)}=\sqrt[]{9.5*10^(-6)}\approx0.003 \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/1awnwxjll1u0falg55nipsj5ogcgn3pj4r.png)
Thus, the standard deviation is approximately 0.003 g/cm³.