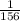Question

There are 13 balls numbered 1 through 13 placed in a bucket. What is the probability of reaching into the bucket and randomly drawing two balls numbered 12 and 2without replacement, in that order? Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.

Answer 1

Explanation

We are given the following:

• 13 balls numbered 1 through 13 placed in a bucket.

We are required to determine the probability of randomly drawing two balls numbered 12 and 2 without replacement, in that order.

This is achieved thus:

The probability of randomly selecting a ball numbered 12 from the bucket is:

`Pr.(12)=(1)/(13)`

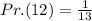
The probability of randomly selecting 2 from the bucket after the first selection is:

`Pr.(2)=(1)/(12)`

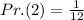
Therefore, the probability of randomly selecting two balls numbered 12 and 2 is:

`\begin{gathered} Pr.=(1)/(13)*(1)/(12) \\ Pr.=(1)/(156) \end{gathered}`

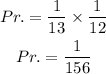
Hence, the answer is:

`(1)/(156)`