Question

Find the slope of the line through the given points.(-4,7) and (-1,-3)Is the slope increasing or decreasing?

Answer 1

• The following formula can be used to find the slope of a line:

`m=(y_2-y_1)/(x_2-x_1)`

These points are on the line:

`(x_1,y_1);(x_2,y_2)`

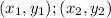
Given the following points:

`\mleft(-4,7\mright);(-1,-3)`

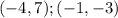
Then, you can set up that:

`\begin{gathered} y_2=-3_{} \\ y_1=7 \\ x_2=-1 \\ x_1=-4 \end{gathered}`

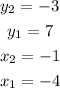
Therefore, substituting values into the formula and evaluating, you get:

`\begin{gathered} m=(-3-7)/(-1-(-4)) \\ \\ m=(-10)/(-1+4) \\ \\ m=-(10)/(3) \end{gathered}`

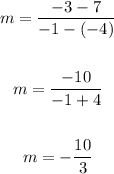
• As you can notice, the slope is negative. Therefore, you can determine that it is decreasing.

Therefore, the answers are:

• Slope of the line:

`m=-(10)/(3)`

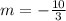
• It is decreasing.