The ordered list of the given plot is:
0, 0, 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7
The first interquartile is given by:
IQ = Q3 - Q1
Where Q3 and Q1:
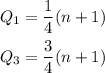
where n = 8 is the total number of data.
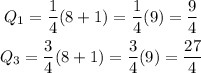
Then, the interquatile range:
IQ = 27/4 - 9/4 = 18/4
Hence, the interquartile range is 18/4