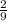Question

A box contains 3 red balls 2 blue balls and 5 white balls a ball is selected and it’s color noted a second ball is selected an it’s color noted find the probability of each of these. 1. P(selecting 2 blue balls) with replacement between the first and second draw2. P(selecting 2 white balls) without replacement between the first and second drawAnswer the questions below show all your work and make sure your answer is in lowest fraction form.

Answer 1

1.

On the first draw, 2 out of the 10 balls are blue. Therefore, the probability of choosing a blue ball is:

`(2)/(10)\rightarrow(1)/(5)`

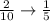
On the second draw, 2 out of the 10 balls are blue, because the drawn blue ball is replaced. Therefore, the probability of choosing a second blue ball is:

`(2)/(10)\rightarrow(1)/(5)`

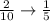
The probability of choosing 2 blue balls in a row, with replacement between the first and second draw, is:

`(1)/(5)\cdot(1)/(5)=(1)/(25)`

Or 4%

ANSWER 1:

`(1)/(25)`

2.

On the first draw, 5 out of the 10 balls are white. Therefore, the probability of choosing a white ball is:

`(5)/(10)\rightarrow(1)/(2)`

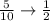
On the second draw, 4 out of the 9 remaining balls are white. Remember that the white ball drawn isn't replaced.

Therefore, the probability of choosing a second white ball is:

`(4)/(9)`

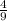
Thereby, the probability of choosing 2 white balls in a row, without replacement between the first and second draw, is:

`(1)/(2)\cdot(4)/(9)=(4)/(18)\rightarrow(2)/(9)`

Or about 22%

ANSWER 2:

`(2)/(9)`