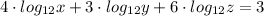Question

a.) Convert the exponential function below to its corresponding logarithmic function. b.) Write the log form from Part A into the expanded log form.

Answer 1

INFORMATION:

We have the next expression:

`12^3=x^4y^3z^6`

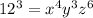
And, we must:

a.) Convert the exponential function below to its corresponding logarithmic function

b.) Write the log form from Part A into the expanded log form

STEP BY STEP EXPLANATION:

a.) To convert it to its corresponding logarithmic function, we must use the next

In our case,

`\begin{gathered} a=3 \\ b=12 \\ n=x^4y^3z^6 \end{gathered}`

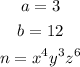
Now, replacing in the formula

`log_(12)(x^4y^3z^6)=3`

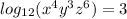
b.) To write the expanded log form of part A, we must use the properties of log

1. We can separate the multiplications using the first property

`\begin{gathered} log_(12)(x^(4)y^(3)z^(6))=3 \\ log_(12)(x^4)+log_(12)(y^3)+log_(12)(z^6)=3 \end{gathered}`

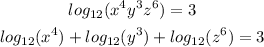
2. We can delete the exponent of the logarithms using the third property

`4\cdot log_(12)x^{\text{ }}+3\cdot log_(12)y+6\cdot log_(12)z=3`

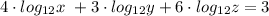
ANSWER:

a.) The logarithmic function would be:

`log_(12)(x^(4)y^(3)z^(6))=3`

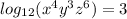
b.) The expanded log form would be:

`4\cdot log_(12)x+3\cdot log_(12)y+6\cdot log_(12)z=3`