Given data:
The first function given is f(x)=2x + 8.
The second function given is h(x) = 2x-8.
The expression for t(x) is,
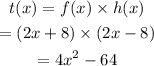
The x-intercepts are the points where y coordinate is zero.
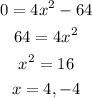
The y-intercepts are the points where x coordinate is zero.
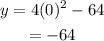
Thus, the zeroes of t(x) are 4, -4, the y-intercept of the graph is (0, -64) and t(x)=4x^2 -64.