Step-by-step explanation
The Fundamental Theorem of Algebra states that:
In this case, we have the quadratic equation:
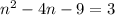
Rewriting this equation, we have the polynomial equal to zero:
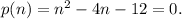
We have a second-order polynomial, so its degree is m = 2 and the Fundamental Theorem of Algebra states that this polynomial has m = 2 roots.
To verify the statement of the Theorem, we solve for n by completing squares.
1) We write the equation as:

2) Summing 2² on both sides of the equation, we have:
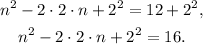
3) We see that both sides can be written as squares:
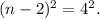
4) Taking the square root on both sides, we get a positive and a negative values:
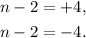
5) Finally, solving for n each equation, we get:
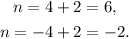
We have found two roots n = 6 and n = -2. We see that the number of roots found is equal to the degree of the polynomial. We conclude that the Fundamental Theorem of Algebra is true.
Answer
The zeros of the quadratic equation are -2, 6.