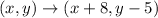Answer:
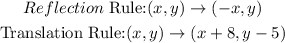
Explanation:
Consider the graph below:
In order to explain this, we use point A as a reference point.
• Point A on the pre-image is located at (3,6).
When A is reflected across the y-axis, its corresponding position is at (-3,6).
Thus, the rule for this reflection is:
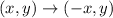
Next, the reflection is followed by a translation right 8 units and down 5 units.

Therefore, the translation rule is: