Question

Need help with the attached - my last tutor and I lost connectivity as we were solving it

Answer 1

`18,24\text{ and 30}`

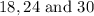
Step-by-step explanation:

Here, we want to get the legs of the triangle

Let the shorter length be x cm

The longer leg will be (x + 6) cm

The hypotenuse length will be (x + 12) cm

According to Pythagoras' theorem. the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides

Thus:

`\begin{gathered} (x\text{ + 12\rparen}^2\text{ = \lparen x\rparen}^2\text{ + \lparen x + 6\rparen}^2 \\ x^2+24x\text{ + 144 = x}^2+12x\text{ + 36 + x}^2 \\ x^2+24x+144\text{ = 2x}^2+12x\text{ + 36} \\ 2x^2-x^2+12x-24x\text{ + 36-144 = 0} \\ x^2-12x\text{ -108 = 0} \end{gathered}`

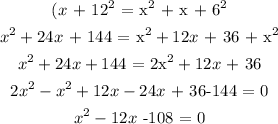
Solving the quadratic equation, we have it that:

`\begin{gathered} x^2-18x+6x-108\text{ = 0} \\ x(x-18)+6(x-18)\text{ = 0} \\ (x+6)(x-18)\text{ = 0} \\ x\text{ = -6 or 18} \end{gathered}`

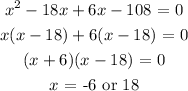
We discard x = -6

This would give us a side length with 0 length

Now, using x = 18:

we have the side lengths as:

18, 18 + 6 and 18 + 12 :

18, 24 and 30