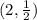Question

Consider the following equation: 6x + 2y = 13A) Write the above equation in the form y = mx + b. Enter the values of m and b in theappropriate boxes below as integers or reduced fractions (in the form A/B.)Answer: y =2 +Preview m: ; Preview b:B) Use your answer in part (A) to find the ordered pair that lies on this line when x = 2.Answer: (2,Enter your answer as an integer or a reduced fraction in the form A/B.

Answer 1

Conider the equation given below;

`6x+2y=13`

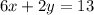
To express this equation in the form

`y=mx+b`

We shall begin by making y the subject of the equation, a follows;

`\begin{gathered} 6x+2y=13 \\ \text{Subtract 6x from both sides;} \\ 6x-6x+2y=13-6x \\ 2y=13-6x \\ \text{Divide both sides by 2, and you'll have;} \\ (2y)/(2)=(13-6x)/(2) \\ y=(13-6x)/(2) \\ \text{Simplify the right side;} \\ y=(13)/(2)-(6x)/(2) \\ y=(13)/(2)-3x \\ \text{Written in the slope-intercept form, it now becomes;} \\ y=-3x+(13)/(2) \end{gathered}`

The values of m and b are;

`\begin{gathered} y=mx+b \\ y=-3x+(13)/(2) \\ \text{Hence;} \\ m=-3,b=(13)/(2) \end{gathered}`

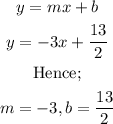
Part B:

Therefore, for a point on this line where x = 2, we would have;

`\begin{gathered} y=-3x+(13)/(2) \\ \text{Substitute for the value of x}=2 \\ y=-3(2)+(13)/(2) \\ y=-6+(13)/(2) \\ y=(13)/(2)-6 \\ \text{Take the LCM of both numbers and we'll now have;} \\ y=(13-12)/(2) \\ y=(1)/(2) \\ \text{Therefore the ordered pair would be;} \\ (2,(1)/(2)) \end{gathered}`

ANSWER:

Part A;

`y=-3x+(13)/(2)`

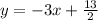
Part B:

`(2,(1)/(2))`