Question

Hii can you help me out with this trigo qn !

Answer 1

The Solution:

Given:

Part(a)

(i) The value of the ratio of

`(\sin\angle PRQ)/(\sin\angle RPQ)`

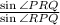
Applying the Law of sine:

`(\sin P)/(p)=(\sin(Q))/(q)=(\sin(R))/(r)`

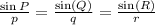
In this case,

So, the ratio

Applying the Law of sine to get the above ratio, we get

`\begin{gathered} (\sin\angle R)/(r)=(\sin P)/(p) \\ \\ Where \\ r=2x \\ p=3x \end{gathered}`

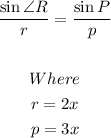
Substituting, we get

Cross multiplying, we get

(ii) To find:

`\cos\angle PQR=\cos\angle Q`

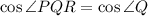
Applying the Law of Cosine:

`\cos\angle PQR=\cos\angle Q=(p^2+r^2-q^2)/(2pr)`

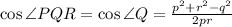
Where,

`p=3x,r=2x,q=4x`

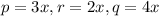
Substituting, we get

`\begin{gathered} \cos\angle Q=((3x)^2+(2x)^2-(4x)^2)/(2(3x)(2x))=(9x^2+4x^2-16x^2)/(12x^2)=(13x^2-16x^2)/(12x^2) \\ \\ \cos\angle Q=(-3x^2)/(12x^2)=(-1)/(4)=-0.25 \\ \\ \angle Q=\cos^(-1)(-0.25)=104.4775\approx104.48^o \end{gathered}`

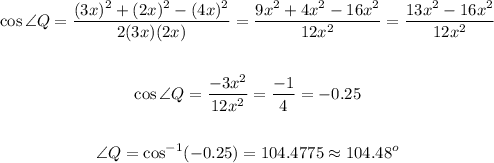
Thus,

`\cos\angle PQR=104.48^o`

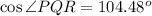
Part (b)

To find the value of x if the area of the triangle PQR is 12 square centimeters.

By area of triangle formula:

`\begin{gathered} Area=(1)/(2)pr\sin Q \\ Where \\ Area=12cm^2 \\ p=3x \\ r=2x \\ \angle Q=104.48^o \end{gathered}`

Substituting these values, we get

`\begin{gathered} 12=(1)/(2)*3x*2x*\sin104.48 \\ cross\text{ multiplying, we get} \\ 24=6x^2(0.96823) \\ 24=5.8094x^2 \end{gathered}`

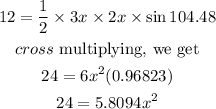
Dividing both sides by 5.8094, we get

`\begin{gathered} x^2=(24)/(5.8094)=4.131235 \\ \text{ Taking the square root of both sides, we get} \\ x=√(4.131235)=\pm2.0325 \\ x=2.0325\text{ \lparen since x cannot be negative\rparen} \end{gathered}`

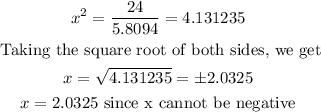
Thus, the value of x is 2.0325