Question

The Wechsler 10 test is normally distributed with a mean of 100 and a standard deviation of 15. Determine the percentage of people scoring at or below 125 on the Wechsler IQ test.

Answer 1

We can calculate this using the z-score of the standard normal distribution (the normal distribution with mean and standard deviation).

The z-value that correspond to a value of 125 can be calculated as:

`z=(X-\mu)/(\sigma)=(125-100)/(15)=(25)/(15)=1.67`

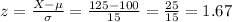
Then, we can calculate the percentage that is below 125 as the probability of being below 125:

`P(X<125)=P(z<1.67)=0.95`

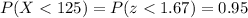
The percentage of people scoring 125 or below is 95%.