Question

f(x) = 12x + 2 - 11x ^ 2 Then the equation of the tangent line to the graph of f(x) at the (0, - 9) is given by y = pi*nx + b for

Answer 1

Given:

`f(x)=12x+2-11e^x`

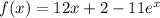
We will find the equation of the line tangent to f(x) at the point (0, -9)

the slope of the tangent line = the first derivative f'(x)

the first derivative will be as follows:

`f^(\prime)(x)=12-11e^x`

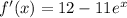
substitute x = 0 to find the slope of the line tangent at (0,-9)

`m=f^(\prime)(0)=12-11e^0=12-11=1`

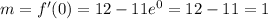
So, the equation of the line will be: y = x - 9

so, the answer will be:

m = 1

b = -9