Let the original number be
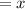
The number decreased by 50% means that we will first calculate 50% of the original number and then subtract it from the original number x

Then, let's subtract the decreased value from the original value
The remaining value will be
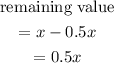
The result is increased by 50% to get
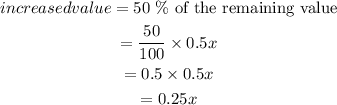
The new value after increasing by 50 % can be gotten by adding the increased value to the remaining value
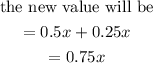
From the question, the new value =99
Therefore, the original value will be
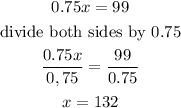
Hence,
The original number = 132