Question

Show all five steps for this hypothesis testing problem. Be sure to give me the null and alternative hypotheses, the test value (z), the p-value, and the conclusion. You can either type your work here, or write it out on paper and submit a scan/picture of your work.A real estate agent compares the selling prices of randomly selected homes in two municipalities in southwestern Pennsylvania to see if there is a difference. The results of the study are shown. Is there enough evidence to reject the claim that the average cost of a home in both locations is the same? Use α = 0.01.

Answer 1

You have to test the hypothesis that the average cost of a home in Scott and Ligonier is equal.

Let X₁ represent the variable "price of a house in Scott Pennsylvania" and X₂ represent the variable "price of a house in Ligonier Pennsylvania".

The working hypothesis can be expressed as:

`\mu_1=\mu_2`

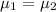
Where

μ₁ is the average population price of the houses on Scott.

μ₂ is the average population price of the houses on Ligonier.

This expression contains the equal sign, this indicates that you have to use it as the null hypothesis of the test. The alternative hypothesis will be its complement, which means that it will state that the average values on both locations are different.

Statistic hypotheses:

H₀: μ₁ = μ₂

H₁: μ₁ ≠ μ₂

The significance level for the test will be 1%. (α=0.01)

Assuming both variables X₁ and X₂ have a normal distribution and considering that the value of the population standard deviations are known, the statistic to use for this test is the standard normal defined as follows:

`Z=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt[]{((\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2))}}N(0,1)`

The data for variables is:

`\begin{gathered} n_1=35;\bar{X_1}=\$93430;\sigma_1=\$5602 \\ n_2=40;X_2=\$98043;\sigma_2=\$4731 \end{gathered}`

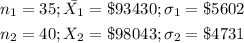
Replace the data in the formula, note that we know the population standard deviations but to calculate the test statistic we need to use the population variances, so I will calculate the square of the standard deviations:

`\begin{gathered} \sigma_1=5602\to\sigma^2_1=5602^2=31382404 \\ \sigma_2=4731\to\sigma^2_2=4731^2=22382361 \end{gathered}`

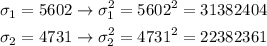
Test statistic:

To compare means we calculate the difference between both means. Under the null hypothesis we stated that both means are equal, which means that their difference will be equal to zero:

`\mu_1-\mu_2=0`

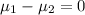
This is the value you have to use for the difference of the population means when you calculate the value of the test statistic.

`\begin{gathered} Z_(H0)=\frac{(93430-98043)-(0)}{\sqrt[]{((31382404)/(35)+(22382361)/(40))}} \\ Z_(H0)=\frac{-4313}{\sqrt[]{1456199.139}} \\ Z_(H0)=-3.82 \end{gathered}`

The p-value of a test is the probability corresponding to the calculated test statistic if possible under the null hypothesis.

For the test statistic Z=-3.82 the corresponding p-value is 0.000133.

To decide whether to reject or not reject a hypothesis test using the p-value, you have to compare this value against the level of significance using the following rule:

- If the p-value ≤ α, reject the null hypothesis.

- If the p-value > α. do not reject the null hypothesis.

For this test, the p-value of 0.000133 is less than the level of significance (α=0.01), so the decision is to reject the null hypothesis.

Since we rejected the null hypothesis, then we can conclude that the population means are different.

When you write a formal conclusion for a hypothesis test, there are several pieces of information that have to be included:

-Level of significance.

-Interpretation of the parameters of the study.

-Decision.

-Populations of the study.

Conclusion:

At a significance level of 1%, the decision is to reject the null hypothesis. This means that the average population price of the houses in Scott Pennsylvania and the average population price of the houses in Ligonier Pennsylvania are different.