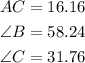Question

If AB has length 10 and BC has length 19, findlength of AC:measure of angle B in degrees:measure of angle C in degrees:Answer should be in degrees and not radians.

Answer 1

Given a right angle triangle ABC

As shown in the figure:

The hypotenuse = BC = 19

One of the legs = AB = 10

We will use the Pythagorean theorem to find the other leg:

`\begin{gathered} AB^2+AC^2=BC^2 \\ 10^2+AC^2=19^2 \\ AC^2=19^2-10^2 \\ AC^2=361-100=261 \\ AC=\sqrt[]{261}=16.16 \end{gathered}`

Now, we will find the measure of the angle B:

`\begin{gathered} \cos B=(adjacent)/(hypotenuse)=(10)/(19) \\ B=\cos ^(-1)(10)/(19)\approx58.24 \end{gathered}`

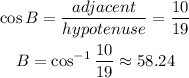
The sum of the angles of the triangle = 180

so, the measure of angle C will be =

`\begin{gathered} 180-(\angle A+\angle B) \\ =180-(90+58.24) \\ =180-148.24 \\ =31.76 \end{gathered}`

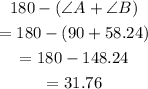
So, as a conclusion to the answer:

`\begin{gathered} AC=16.16 \\ \angle B=58.24 \\ \angle C=31.76 \end{gathered}`