Question

4#The mean diastolic blood pressure for a random sample of 60 people was 81 millimeters of mercury. If the standard deviation of individual blood pressure readings is known to be 8 millimeters of mercury, find a 95% confidence interval for the true mean diastolic blood pressure of all people. Then give its lower limit and upper limit.Carry your intermediate computations to at least three decimal places. Round your answers to one decimal place. (If necessary, consult a list of formulas.)Lower limit:??Upper limit: ??

Answer 1

In this case we want to estimate the mean of the population; since the sample size is larger than 60 and we know the standard deviation of the population the confidence interval is given by:

`\begin{gathered} \bar{x}\pm z\sigma_{\bar{x}} \\ \text{ where} \\ \sigma_{\bar{x}}=(\sigma)/(√(n)) \end{gathered}`

Now, from a normal distribution table we know that the z-value for a 95% confidence interval is 1.96; plugging these and the values of the mean and standard deviation given we have that:

`81\pm(1.96)((8)/(√(60)))=81\pm2.024`

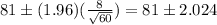
Choosing the negative sign we can calculate the lower limit:

`81-2.024=79`

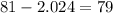
Choosing the positive sign we can calculate the upper limit:

`81+2.024=83`

Threfore, the lower and upper limits of the confidence interval are 79 and 83, respectively.