Question

A scale drawing for an apartment is shown below. In the drawing, 4 cm represent 5m. Assuming the bedroom is rectangular, find the area of the real bedroom.

Answer 1

To solve this question, follow the steps below.

Step 01: Find the real measures of the bedroom.

Given the measure in the drawing: 8 cm x 12 cm.

Given the scale: 4 cm = 5 m.

We can use proportion to find the real measures.

First side:

`(4cm)/(5m)=(8cm)/(x)`

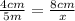
Multiplying both sides by x*5m

`\begin{gathered} (4cm)/(5m)*x*5m=(8cm)/(x)*x*5m \\ 4cm*x=8cm*5m \end{gathered}`

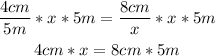
Diving both sides by 4cm:

`\begin{gathered} (4cm)/(4cm)*x=(8cm*5m)/(4cm) \\ x=2*5m \\ x=10m \end{gathered}`

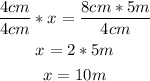
Second side:

Doing the same steps for the second side:

`\begin{gathered} (4cm)/(5m)=(12cm)/(x) \\ (4cm)/(5m)*x*5m=(12cm)/(x)*x*5m \\ 4cm*x=12cm*5m \\ (4cm)/(4cm)*x=(12cm*5m)/(4cm) \\ x=15m \end{gathered}`

The measures of the real bedroom are 10m x 15m.

Step 02: Find the area of the bedroom.

The area (A) of the bedroom is the area of a rectangle and can be found by multiplying the sides.

`\begin{gathered} A=10*15 \\ A=150m^2 \end{gathered}`

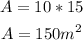
Answer: The area of the real bedroom is 150 m².