Step-by-step explanation
From the image, we will have the sides of the quadrilateral as:
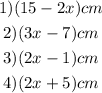
Part I
Therefore, the perimeter of the quadrilateral is the sum of all the sides. This is given as
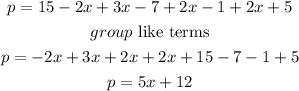
Answer: (5x+12) cm
Part II
Since the perimeter of the quadrilateral is 32cm. Therefore,
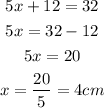
From the image it is clear that the longest side is 2x+5, we can then convert this to its actual length value.
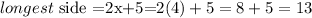
Answer: 13cm