Question

Solve for x.6x = 2x³ + 11x²x = [?], [ ], [ ]Order your answers from smallest tolargest. Enter the number that belongs inthe green box.Note: Enter any fractional answers in decimal form.

Answer 1

Given the equation:

`6x=2x^3+11x^2`

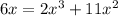
Let's solve the equation for x.

Rearrange the equation:

`2x^3+11x^2=6x`

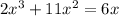
Subtract 6x from both sides:

`\begin{gathered} 2x^3+11x^2-6x=6x-6x \\ \\ 2x^3+11x^2-6x=0 \end{gathered}`

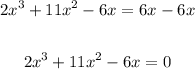
Now, let's factor the left side of the equation.

Factor out x from all terms:

`x(2x^2+11x-6)=0`

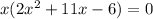
The next step is to factor by grouping.

We have:

`\begin{gathered} x(2x^2-1x+12x-6)=0 \\ \\ x((2x^2-1x)(12x-6))=0 \end{gathered}`

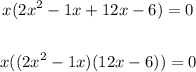
factor out x from the first group and factor out 6 from the second group:

`\begin{gathered} x(x(2x-1)+6(2x-1))=0 \\ \\ x((x+6)(2x-1))=0 \\ \\ x(x+6)(2x-1)=0 \\ \end{gathered}`

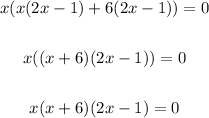
Thus, we now have the solutions:

`\begin{gathered} x=0 \\ x+6=0 \\ 2x-1=0 \end{gathered}`

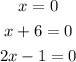
Solve each factor for x.

We have:

`\begin{gathered} x=0 \\ \\ \\ x+6=0 \\ \text{ Subtract 6 from both sides:} \\ x+6-6=0-6 \\ x=-6 \\ \\ \\ 2x-1=0 \\ Add\text{ 1 to both sides:} \\ \text{ 2x - 1 + 1 = 0+1} \\ 2x=1 \\ \text{ Divide both sides by 2:} \\ (2x)/(2)=(1)/(2) \\ x=0.5 \end{gathered}`

Therefore, the solutions are:

x = -6, 0, 0.5

ANSWER:

x = -6, 0, 0.5