first, notice that angles POS and ROS are supplementary, then:
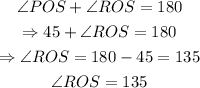
then, we can use the equation of the area of a circle sector:
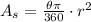
in this case, we have that the diameter is RP = 8, then the radius is r = RP/2 = 4, then, using the formula and knowing that the angle of the shaded area measures 135 degrees, we get:
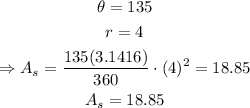
therefore, the area of the shaded sector is 18.85 square units