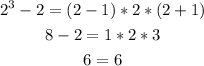Question

Observe that: 6= 1 X2 X3; 24 = 2 X 3 X 4; 60 = 3 X 4 X 5 - Note also that: 6 = 23 - 2 ; 24 = 33 - 3 ; 60 = 43 - 4 (a) Write down the first number larger than 60 that is the product of three consecutive integers. (b) Write down the smallest 4-digit number that is the product of three consecutive integers. (c) Prove algebraically that any number that can be written in the form n - n can be expressed as the product of three consecutive integers.

Answer 1

a) 120

b) 1320

c)

`\begin{equation*} n^3-n=(n-1)*n*(n+1) \end{equation*}`

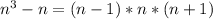
Step-by-step explanation:

Given:

a) From the above, we can see the first three numbers that are products of three consecutive integers. The numbers are 6, 24, and 60.

The next number will be;

`120=4*5*6`

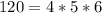
So the first number that is larger than 60 that is the product of three consecutive numbers is 120

b) The first 4-digit number that is a product of three consecutive integers is 1320 as can be seen below;

`1320=10*11*12`

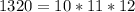
So 1320 is the smallest 4-digit number that is the product of three consecutive integers.

c) We can go ahead and prove as shown below;

`\begin{gathered} n^3-n=n(n^2-1)=n(n^2-1^2)=n(n+1)(n-1)=(n-1)*n*(n+1) \\ \therefore n^3-n=(n-1)*n*(n+1) \end{gathered}`

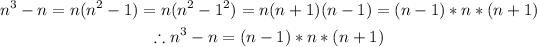
For example, if n = 2, we'll have;

`\begin{gathered} 2^3-2=(2-1)*2*(2+1) \\ 8-2=1*2*3 \\ 6=6 \end{gathered}`