Question

A teacher purchased 20 calculators and 10 measuring tapes for her class and paid $495.Later, she realized that she didn't order enough supplies. She placed another order of 8 ofthe same calculators and 1 more of the same measuring tape and paid $178.50.This system represents the constraints in this situation:20c + 10m = 4958c + m = 178.501. Discuss with a partner:a. In this situation, what do the solutions to the first equation mean?b. What do the solutions to the second equation mean?c. For each equation, how many possible solutions are there? Explain how youknow.d. In this situation, what does the solution to the system mean?2. Find the solution to the system. Explain or show your reasoning.3. To be reimbursed for the cost of the supplies, the teacher recorded: "Itemspurchased: 28 calculators and 11 measuring tapes. Amount: $673.50."a. Write an equation to represent the relationship between the numbers ofcalculators and measuring tapes, the prices of those supplies, and the totalamount spent.b. How is this equation related to the first two equations?c. In this situation, what do the solutions of this equation mean?

Answer 1

1. a.

The solution for the first equation means all possible combinations of prices for calculators and tapes that would make a final cost of $495 for 20 calculators and 10 tapes.

b.

The solution for the second equation means all possible combinations of prices for calculators and tapes that would make a final cost of $178.5 for 8 calculators and 1 tape.

c.

Since each equation has 2 variables, there is an infinite number of solutions for each equation individually. Because we can choose any value of c and calculate the corresponding value of m to solve the equation.

d.

The solution to the system means an unique pair of values (one value for c and one for m) that satisfies both equations at the same time.

2.

In order to find the solution of the system, let's first solve the second equation for m and then use its value in the first equation:

`\begin{gathered} 8c+m=178.5\to m=178.5-8c \\ 20c+10m=495 \\ 20c+10(178.5-8c)=495 \\ 20c+1785-80c=495 \\ -60c=495-1785 \\ -60c=-1290 \\ c=21.5 \\ \\ m=178.5-8\cdot21.5 \\ m=178.5-172 \\ m=6.5 \end{gathered}`

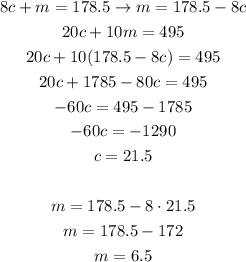
Therefore the calculator costs $21.50 and the tape costs $6.50.

3. a.

28 calculators and 11 tapes cost $673.50, so we have the equation:

`28c+11m=673.5`

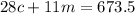
b.

This equation has the same solution as the other two equations.

c.

The solution for this equation means all possible combinations of prices for calculators and tapes that would make a final cost of $673.50 for 28 calculators and 11 tapes.