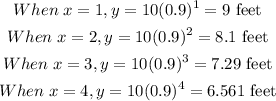Answer:
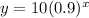
Step-by-step explanation:
The ball is dropped from an initial height of 10 feet.
It loses 10% of its height after every bounce.
• An equation for the height of the ball, y, after x bounces is derived below:
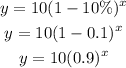
Substitute the values of x=1,2,3 and 4 respectively: