Step-by-step explanation
Given: The pet groomer charges according to the dog weights as follows:
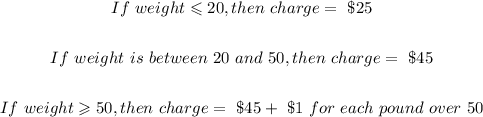
Required: To match each piece of the piecewise function with the corresponding restriction.
This is achieved thus:
==> For the first function
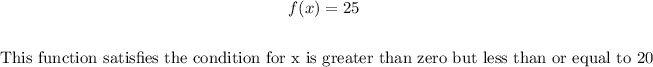
==> For the second function
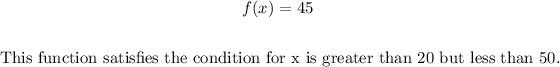
==> For the third function
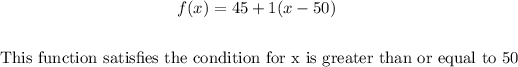
Hence, the answers are:
f(x) = 25 ==> 0 less than x less than or equal to 20
f(x) = 45 ==> 20 less than x less than 50
f(x) = 45 + 1(x - 50) ==> x greater than or equal to 50.