The functions are given as shown:
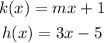
The question also provides:
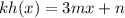
The expression kh(x) represents a composite of functions such that:
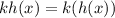
Let us evaluate the value of the composite of the functions:
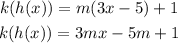
Therefore, we can equate the given value of kh(x) and the derived one:

Hence, we can solve for m in the equation above by collecting like terms on opposite ends of the equality sign and get our answer:
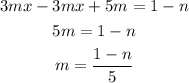
The answer is:
