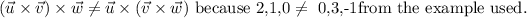Question

if vectors u=4, v=6 and w=3 prove that(⃗ × ) × ⃗ = ⃗ × ( × ⃗ )(they are supposed to all have arrows over them but it’s not fully working)

Answer 1

Given:

`(\vec{u}*\vec{v})*\vec{w}=\vec{u}*\vec{(v}*\vec{w})`

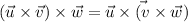
u has direction ( 1, 0,0)

v has directions (1, 1,0)

w has directions(1, -2,1)

`(0,0,1)*\vec{w}\Rightarrow\begin{bmatrix}{i} & {j} & {k} \\ {0} & {0} & {1} \\ {1} & {-2} & {1}\end{bmatrix}\Rightarrow i(0--2)-j(0-1)+k(0)\Rightarrow(2,1,0)`

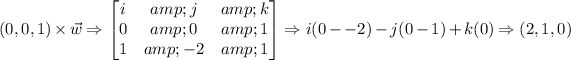
So (2,1,0) is the left hand side. The cross product gives us a direction between two vectors or the coordiantes it pointing to.

The right hand side:

`\vec{u}*(\vec{v}*\vec{w})\Rightarrow\vec{u}*\begin{bmatrix}{i} & {j} & {k} \\ {1} & {1} & {0} \\ {1} & {-2} & {1}\end{bmatrix}\Rightarrow\vec{u}*(i\begin{bmatrix}{1} & {0} \\ {-2} & {1}\end{bmatrix}-j\begin{bmatrix}{1} & {0} \\ {1} & {1}\end{bmatrix}+k\begin{bmatrix}{1} & {1} \\ {1} & {-2}\end{bmatrix})`
`\vec{u}*(i(1-0)-j(1-0)+k(-2-1))\Rightarrow\vec{u}*(1,-1,-3)`
`\vec{u}*(1,-1,-3)\Rightarrow\begin{bmatrix}{i} & {j} & {k} \\ {1} & {0} & {0} \\ {1} & {-1} & {-3}\end{bmatrix}\Rightarrow i\begin{bmatrix}{0} & {0} \\ {-1} & {-3}\end{bmatrix}-j\begin{bmatrix}{1} & {0} \\ {1} & {-3}\end{bmatrix}+k\begin{bmatrix}{1} & {0} \\ {1} & {-1}\end{bmatrix}`
`i(0-0)-j(-3-0)+k(-1-0)\Rightarrow(0,3,-1)`

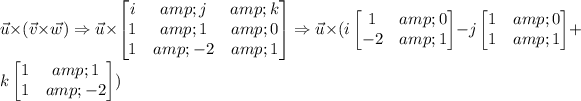
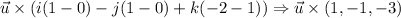
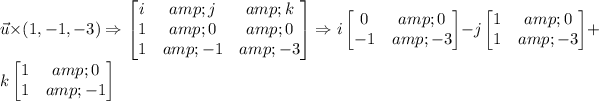
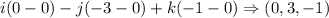
So using (u x v) x w = u x (v x w) on the left hand side we got (2,1,0) and the right hand side we got (0,3,-1)

Therefore we have (2,1,0) = (0,3,-1) which can't be possible.

Answer:

`(\vec{u}*\vec{v})*\vec{w}\\e\vec{u}*(\vec{v}*\vec{w})\text{ because \lparen2,1,0\rparen }\\e\text{ \lparen0,3,-1\rparen from the example used.}`