Step-by-step explanation
We have μ = 144 and sd = 13
Computing the needed probabilities:
a) P(x < 137 ) =
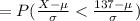
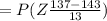
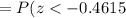
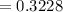
a) The probability is 0.3228
b) Number of runners ---> n=10
P(x < 137 ) =
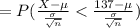
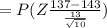
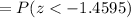
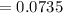
b) The probability is 0.0735
c) Number of runners ---> n=50
P(x < 137 ) =
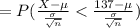
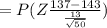
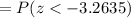

b) The probability is approximately 0.0006