Question

The directions are with the pic below. I have to send part 2 of choices. Couldn’t all fit .

Answer 1

ANSWER and EXPLANATION

When a point is rotated 180 degrees counterclockwise (with the origin as the center of rotation), the coordinates of the point changes as follows:

`(x,y)\to(-x,-y)`

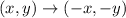
Hence, the coordinates for the triangle S'T'U' will be:

`\begin{gathered} S(-1,3)\to S^(\prime)(1,-3) \\ T(-4,3)\to T^(\prime)(4,-3) \\ U(-3,1)\to U^(\prime)(3,-1) \end{gathered}`

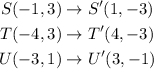
Let us plot that:

That is the answer.