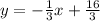Step-by-step explanation
We must find the equation of the line that:
0. passes through the point (x₀, y₀) = (-11, 9),
,
1. and it is parallel to the line:
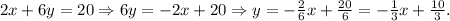
(1) The general point-slope equation of a line that passes through a point with coordinates (x₀, y₀) is:
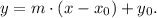
Where m is the slope.
Replacing the coordinates (x₀, y₀) = (-11, 9), we have:
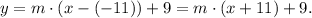
(2) The general slope-intercept equation of a line is:
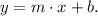
Comparing this equation with the equation from point 2, we identify the slope:
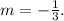
The line that passes through (x₀, y₀) = (-11, 9) must have a slope m = -1/3 too because it is parallel to this line. Replacing the value m = -1/3 in the last equation of (1), and then simplifying, we get:
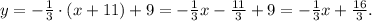
Answer