Since two side sides of the triangle and an angle is known, we apply the Cosine rule
Formula for Cosine rule is given below,
Where a is distance between the house and pier,
b is the distance between the house and restaurant,
c is the distance between the pier and the restaurant,
C is the angle opposite c
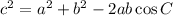

Substituting the variables into the given formula above,
![\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ c^2=(1.2)^2+(1.9)^2-2(1.2)(1.9)\cos 87^0 \\ c^2=1.44+3.61-4.56(0.05234) \\ c^2=5.05-0.2387 \\ c^2=4.8113 \\ \sqrt[]{c^2}=\sqrt[]{4.8113} \\ c=2.1935\text{ miles} \\ c\approx2.19\text{ miles} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7e4c6w83fpd1ksdduyjf7y8c76xob6mxug.png)
Hence, the distance from the pier to the restaurant is 2.19 miles.