Question

Question 5Look at the graph of the equation y = x2– 2x - 7.how does this graph compare with the graph of the equation in question 1?

Answer 1

The graph is the same. Even though the equations have different forms, they are still equivalent.

Explanation:

i re wrote it

Answer 2

We can rewrite the equation into its vertex form, as shown below

`\begin{gathered} y=x^2-2x-7 \\ y=a(x-h)^2+k \\ \Rightarrow y=ax^2-2ah+ah^2+k \\ \Rightarrow\begin{cases}a=1 \\ -2ah=-2\Rightarrow h=1 \\ ah^2+k=-7\Rightarrow1+k=-7\Rightarrow k=-8\end{cases} \end{gathered}`

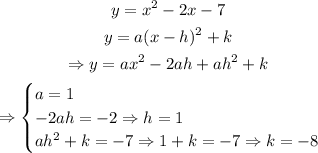
Therefore, the vertex form of y=x^2-2x-7 is

`y=(x-1)^2-8`

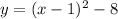
On the other hand, the graph of the equation of question 1 seems to be the same graph like the one of the function y=x^2-2x-7. The y-intercept is the same (0,-7) and the vertex seems to be located on the same point (1,-8).

The two graphs are the same, only the scale changes.

These two graphs are the same.