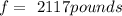Question

The lifting force, F, exerted on an airplane wing varies jointly as the area, A, of the wing's surface andthe square of the plane's velocity, v. The lift of a wing with an area of 290 square feet is 3000 poundswhen the plane is going 250 miles per hour. Find the lifting force on the wing if the plane slows downto 210 miles per hour. (Leave the variation constant in fraction form or round to at least 5 decimalplaces. Round off your final answer to the nearest pound.)

Answer 1

Given that:

`f\alpha av^2`

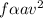
Hence, the equation relating them is

`f=kav^2`

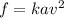
where,

f is the lifting force.

k is the constant of variation.

a is the area of the wing's surface.

v is the velocity of the plane.

Given

`\begin{gathered} f=3000pounds \\ a=290ft^2 \\ v=250milesperhour \end{gathered}`

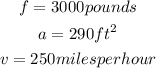
Solving for k

`k=(f)/(av^2)=(3000)/(290*250^2)=(3)/(18125)`

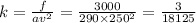
Now that you know k, you can solve the problem.

Let us now solve for f

Therefore,

`\begin{gathered} a=290squarefeet \\ v=210milesperhour \\ \therefore f=(3)/(18125)*290*210^2=2116.80000pounds \end{gathered}`

Hence, the answer is

`f=\text{ }2117pounds`