Question

Cancer Chance The American Cancer Society website states that a person'slifetime chance of developing cancer is 42%. Consider a group of 4 randompersons. Find the probability of each of the following outcomes.(a) None of the 4 develops cancer in their lifetime.(b) 3 out of the 4 persons develops cancer in their lifetime.Nuestion Heln: Message instructor

Answer 1

The Solution.

First, we state the probability of developing cancer in a lifetime and that of not developing cancer in a lifetime.

`\begin{gathered} \text{Prob(Cancer) =}0.42 \\ \text{Prob(no cancer}=(1-0.42)=0.58 \end{gathered}`

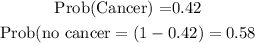
a. None of the 4 develop cancer:

Possible outcomes=[C'C'C'C']

`\begin{gathered} P(C^(\prime)C^(\prime)C^(\prime)C^(\prime))=pr(C^(\prime))* Pr(C^(\prime))* Pr(C\text{)}* Pr(C^(\prime))=Pr(C^(\prime))^4 \\ \text{Where Pr(C')=probability of not developing cancer.} \\ \text{ =0.58}^4=0.11316\approx0.113(11.3\text{ \%)} \end{gathered}`
`\begin{gathered} Pr(C^{}\text{C}C^{}C^(\prime))=Pr(C)* Pr(C)* Pr(C)* Pr(C^(\prime))=Pr(C)^3* Pr(C^(\prime)) \\ =0.42^3*0.58=0.0741*0.58=0.04297\approx0.043\text{ ( 4.3\%)} \end{gathered}`

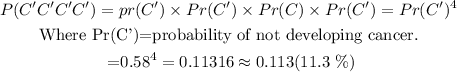
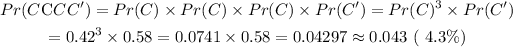
Therefore, the correct answers are;

a. 0.113 (or 11.3%)

b. 0.043 (or 4.3%)