EXPLANATION
Let's see the facts:
We have a sequence here as follows:
First pattern: 12 sticks
Second pattern: 19 sticks
Third pattern: 26 sticks
Given the sequence:
12, 19, 26
The nth term is obtained by applying the following formula.

Check wheter the difference is constant:
Compute the difference of all the adjacent terms:

19-12 = 7 , 26-19=7
The difference between all of the adjacent terms is the same and equal to d=7
The first element of the sequence is:
a_1=12
Therefore, the nth term is computed by:
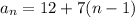
So, when n=91, the number of sticks are:
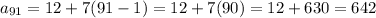
Thus, there are 642 sticks in the 91st pattern.