Question

Solving a percent make sure problem using a system of linear equations

Answer 1

We have to make a 170 gallons mixture of antifreeze with a 40% antifreeze percentage.

We have to made it mixing products from two brands:

• First brand (F): 35% pure antifreeze

,

• Second brand (S): 85% pure antifreeze.

NOTE: To work with percentage and perform calculations, it is better to express the percentages in decimal form. We can do this by dividing the percentage by 100. Then, for example, 35% will become 0.35.

We will call F to the volume for the first brand and S to the volume of the second brand.

We know that the total mixture volume is 170 gallons. The volume is made of the mixture fo the volume of the first brand and the volume of the second brand. Then, this total volume is equal to the sum of F and S, so we can write:

`F+S=170`

We need another equation to have a complete system of equations (two equations for two unknowns).

We can use the antifreeze content to write one.

We know the the mixture has to have 40% pure antifreeze. Then, the volume of antifreeze will be 40% of the total volume of 170 gallons.

This volume of antifreeze will come from 35% of the volume of the first brand and 85% of the volume of the second brand.

Then, we can write:

`\begin{gathered} 0.35*F+0.85*S=0.40*170 \\ 0.35F+0.85S=68 \end{gathered}`

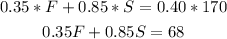
We now have can use the first equation to express S in function of F:

`\begin{gathered} F+S=170 \\ S=170-F \end{gathered}`

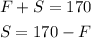
We can now replace S in the second equation and solve for F:

`\begin{gathered} 0.35F+0.85S=68 \\ 0.35F+0.85(170-F)=68 \\ 0.35F+144.5-0.85F=68 \\ 0.35F-0.85F=68-144.5 \\ -0.5F=-76.5 \\ F=(76.5)/(0.5) \\ F=153 \end{gathered}`

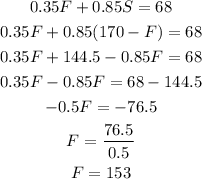
We have found that the first brand will have a volume in the mixture of 153 gallons.

We can now calculate S as:

`\begin{gathered} S=170-F \\ S=170-153 \\ S=17 \end{gathered}`

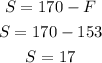
The second brand volume in the mix is 17 gallons.

Answer:

First brand: 153 gallons

Second brand: 17 gallons.