Question

Could you please answer these and show me how to get to the answers?

Answer 1

Given the function:

`y=x^2-4x-5`

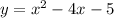
- Factor to find the x-intercept:

Factor and equal to zero for Vertexeach factor.

`x^2-4x-5=(x-5)(x+1)`

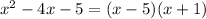
So:

`\begin{gathered} x-5=0 \\ x=5 \\ \text{and} \\ x+1=0 \\ x=-1 \end{gathered}`

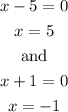
a) The vertex of a parabola is:

`x=-(b)/(2a)`

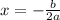
The parameters of the parabola are:

a = 1, b = -4 and c = -5

`x=-(-4)/(2(1))=(4)/(2)=2`

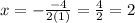
We find y:

`y=(2)^2-4(2)-5=4-8-5=-9`

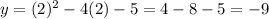
Therefore the vertex of the parabola is: (2, -9)

b) x-intercepts are: (5,0) and (-1,0)

c) Vertex: (2, -9)

d) Graph:

- Table:

x y

-1 0

0 -5

1 -8

2 -9

3 -8

4 -5

5 0

6 7