Question

4. The area of the base of the regular quadratic pyramid SABCD is 25 cm2 and the area of the side wall SAB is 15 cm2. Calculate: 1) the length of the base edge; 2) the length of the diagonal of the base; 3) the length of the apothem; 4) the length of the side edge;

Answer 1

1) 5 cm

2) 7.07 cm

3) 6 cm

4) 6.5 cm

Explanation:

Part 1:

Since we're looking at a square pyramid, we'll have that the area of the base is the area of a square:

`A_b=L^2`

Since we know this area is 25 square centimiters, we can find L as following:

`\begin{gathered} 25=L^2 \\ \rightarrow L=√(25) \\ \\ \Rightarrow L=5 \end{gathered}`

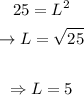
Therefore, we can conlcude that the length of the base edge is 5 cm

Part 2:

The lenght of the diagonal of a square is given by the formula:

`D=√(2)\text{ }L`

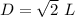
Where L is the lenght of the sides of the square. Since we've already calculated this lenght, we can find the lenght of the diagonal as following:

`\begin{gathered} D=(√(2))(5) \\ \\ \Rightarrow D=7.07 \end{gathered}`

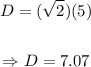
This way, we can conclude that the length of the diagonal of the base is 7.07 cm

Part 3:

Let's take a look at a drawing of side wall SAB:

Remember that the formula used to calculate the area of a triangle is:

`A_t=(bh)/(2)`

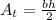
Where:

• b, is the base of the trianlge

,

• h, is the height of the triangle. In this case, the apothem ,(a)

Since we already know this area, we can find a as following:

`\begin{gathered} 15=(5* a)/(2)\rightarrow30=5a\rightarrow(30)/(5)=a \\ \\ \Rightarrow a=6 \end{gathered}`

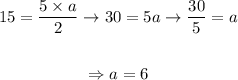
This way, we can conlcude that the length of the apothem is 6 cm

Part 4:

Now we know the apothem, let's take another look at side wall SAB:

We can extract from here the following right triangle:

Using the pythagorean theorem, we'll have that :

`l^2=2.5^2+6^2`

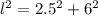
Solving for l,

`\begin{gathered} l=√(2.5^2+6^2) \\ \\ \Rightarrow l=6.5 \end{gathered}`

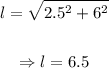
Therefore, we can conlcude that the length of the side edge is 6.5 cm