Question

Write the equation of a Circle with the given information.Center: (-14,9) Point on the Circle: (-11, 12)

Answer 1

The equation of a circle with center (a, b) and radius r is

`(x-a)^2+(y-b)^2=r^2`

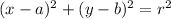
We are given the center as

`(a,b)\Rightarrow(-14,9)`

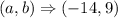
To find the radius, we can use the formula to find the distance between two points, that is, the point on the circle and the center.

`r=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2_{}_{}}`

where (x₁, y₁) = (-14, 9)

(x₂, y₂) = (-11, 12)

Thus, we have

`\begin{gathered} r=\sqrt[]{(12-9)^2+(-11-\lbrack-14\rbrack)^2} \\ r=\sqrt[]{3^2+3^2} \\ r=\sqrt[]{9+9} \\ r=\sqrt[]{18} \\ r=3\sqrt[]{2} \end{gathered}`

Therefore, inputting all the values into the equation for a circle, we have

`\begin{gathered} (x-\lbrack-14\rbrack)^2+(y-9)^2=3\sqrt[]{2} \\ \therefore \\ (x+14)^2+(y-9)^2_{^{}}=3\sqrt[]{2} \end{gathered}`